UCSP

The dance is called Zapin Tenglu, one of the many types of zapin dances in Malaysia.
This type of zapin dance is originated from the state of Johor and among the most popular Malay folk dance in Malaysia.

The dancers in this performance are those professional zapin dancers from Johor's Heritage Foundation funded by the State of Johor Government (Yayasan Warisan Johor), needless to say one of the best professional folk dancers group in the country and the Asean region! 

Zapin or zafin was introduced to Malay archipelagos hundred of years ago by Arab traders who came here to trade and at the same time expand the teachings of Islam. After sometimes, the dance revolved to inculcate the values and tradition of the local Malay people until it wholly become unique in its own local way but still maintaining some important features of original Arabic zapin dance like the musical instruments used (gambus / oud, traditional drums etc.), the Middle East melody in its song and the identical 8-counting-basic-movements in its dance steps!

Apart from the Malaysia's state where the zapin is danced by its people like Johor, Kedah, Terengganu, Kelantan, Sarawak and Sabah, zapin is also danced by the people in its neighboring country like Singapore, Indonesia and Brunei.

inverse function

• Find the inverse of y = x² + 1, x > 0, and determine whether the inverse is a function.
     

You'll notice that the only difference between this and the previous exampleis that the domain has been restricted to the positive x-axis this time. Here's the graph: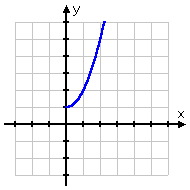

Since this passes the Horizontal Line Test, I know that its inverse will be a function. And since this graph is different from that of the previous function, I know that the inverse must be different. Again, it is very helpful to first find the domains and ranges. The function's domain isx > 0; the range (from the graph) is y > 1. Then the inverse's domain will be x > 1 and the range will be y > 0. Here's the algebra:  Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved


The original function:
I'll solve for "x =":
Since I already figured out the domain and range, I know that I have to choose the positive square root:
Now I'll switch the x's and y's; the new "y =" is the inverse:

Here's the graph:

Here's the graph:

Then the inverse is  y = sqrt(x – 1), x > 1, and the inverse is also a function.

If you've studied function notation, you may be starting with "f(x)" instead of "y". In that case, start the inversion process by renaming f(x) as "y"; find the inverse, and rename the resulting "y" as "f^–1(x)". It's usually easier to work with "y". Warning: This notation is misleading; the "minus one" power in the function notation means "the inverse function", not "the reciprocal of". Don't confuse the two.

• Find the inverse of  y = ^–2 / _{(x – 5)}, and determine whether the inverse is also a function.
Since the variable is in the denominator, this is a rational function. Here's the algebra:


The original function:
I multiply the denominator up to the left-hand side of the equation:
I take the y through the parentheses:
I get the x-stuff by itself on one side of the "equals" sign:
Then I solve for x:
And then switch the x's and y's:

This is just another rational function. The inverse function is y =  ^{(5x – 2)} / _x

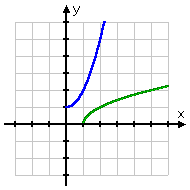
• Find the inverse of f(x) = –sqrt(x – 2), x > 2. Determine whether the inverse is also a function, and find the domain and range of the inverse.
     

The domain restriction comes from the fact that x is inside a square root. Usually I wouldn't bother writing down "x > 2", because I know that x-values less than2 would give me negatives inside the square root. But the restriction is useful in this case because, together with the graph, it will help me determine the domain and range on the inverse:

The domain is x > 2; the range (from the graph) is y < 0. Then the domain of the inverse will bex < 0; the range will be y > 2. Here's the algebra:


The original function:
Rename "f(x)" as "y":
Solve for "x =":
Switch x and y:
Rename "y" as "f-inverse".  Since I already figured out the domain and range, I know which half of the quadratic I have to choose:

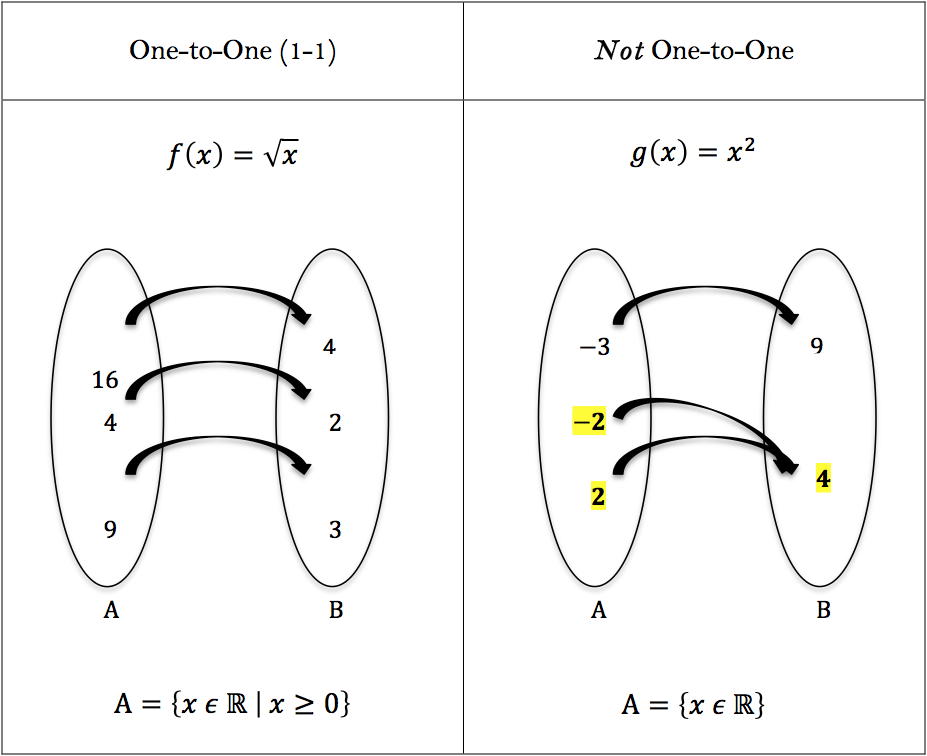
one-to-one function MATH

One-to-One Functions

Part 1. What is a one-to-one function?

A function f with domain A is called a one-to-one function if every f(x)-value in the range B comes from only one x-value in A. 
(i.e. Every element in A is mapped/connected to a unique element in B.) 

Formally stated: f is 1−1 if and only if for some x1,x2∈A,

f(x1)=f(x2)impliesthatx1=x2.

Example.

Graphically, we can determine if a function is 1−1 by using the Horizontal Line Test, which states: A graph represents a 1−1 function if and only if every horizontal line intersects that graph at most once. 

Consider the graphs of the functions given in the previous example: 

1. f(x)=x√ 

From the graph it’s clear that f(x) is 1−1. This is because every horizontal line (such as the line y=1) intersects the graph at most once. More specifically, if a point of intersection exists between f(x) and the line y=c, it is of the form (c,c√). 

2. g(x)=x2 

From the graph we can see that g(x) is not 1−1, because the horizontal line y=1 intersects the graph at (1,1)  and (−1,1). In general, every horizontal line y=c that intersects the graph, intersects it at (c√,−c) and (−c√,−c) , except at the vertex (0,0). 

Part 2. Verifying that a function is 1-1

When we say "verify", we generally mean "prove." To prove that a function is 1−1, we can't just look at the graph, because a graph is a small snapshot of a function, and we generally need to verify 1−1-ness on the whole domain of a function. So though the Horizontal Line Test is a nice heuristic argument, it's not in itself a proof. For proofs, we have two main options to show a function is 1−1: 

Option 1.

Show that if f(x1)=f(x2), then x1=x2. 

This statement says in words: "If the function has the same value at two points, then the points must be the same." In other words, "If the function has the same value at two points, the points can't be different." And the final rewording is, "The function can't give the same value to two different points." 

Thus, this short mathematical statement is precisely the Horizontal Line Test! The graph is 1−1 if there are no two x-values which get assigned the same y-value! 

Now, let's use this statement to prove a function is 1−1: 

Example. Show that f(x)=1x is 1−1.

Assume that there exists some x1 and x2, such that f(x1)=f(x2). i.e. 1x1=1x2.

But, 1x1=1x2⇒1x1−1x2=0⇒x1−x2x1x2=0⇒ the numerator must equal zero! i.e. x2−x1=0⇒x2=x1

Option 2.

To show a function is 1−1, we can show that a function is always increasing or always decreasing. Consequently, it will always pass the Horizontal line test! 

Recall the following definitions: 

A function f is increasing on its domain if whenever x1<x2, then f(x1)<f(x2). 
i.e. as x gets larger, f(x) also gets larger. 

A function f is decreasing on its domain if whenever x1<x2, then f(x1)>f(x2). 
i.e. as x gets larger, f(x) gets smaller. 

Example. Show that f(x)=x3 is 1−1.

We know that for a,b∈R, if a<b⇒f(a)=a3<b3=f(b). Therefore, f(x)=x3 is an increasing function on its domain, R. This can also be verified by the graph (below): 

Therefore, every horizontal line y=c will only intersect the graph at the point (c,c3).